CSCI 3322 (Principles of Algorithms), Fall 2022:
Homework 2
- Credit:
- 20 points.
Be sure you have read, or at least skimmed, Chapter 3 of the textbook.
Answer the following questions. You may write out your answers by
hand and scan them, or you may use a word processor
or other program, but please turn in a PDF or plain text file.
(No links to shared files on Google Drive please, and no word-processor files.)
Turn it in by putting it in your course “TurnIn” folder on
Google Drive.
Please be sure to include your name somewhere in the file,
so when I print it for grading I know whose work it is.
(With the pledge is fine.)
- (10 points)
Prove Theorem 3.1 in the textbook.
(Recall that proving something of the form “
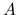 if and only if
if and only if 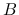 ”
means you have to prove “if
”
means you have to prove “if 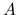 then
then 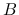 ” and “if
” and “if 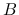 then
then 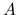 ”.)
Hint: If you write down the formal definitions of
“
”.)
Hint: If you write down the formal definitions of
“
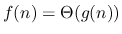 ”,
“
”,
“
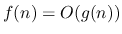 ”, and
“
”, and
“
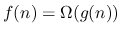 ”,
I think there is not much more to do.
”,
I think there is not much more to do.
- (10 points)
Is
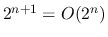 ?
Is
?
Is
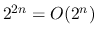 ?
Justify your answers.
(For either you think is
?
Justify your answers.
(For either you think is 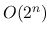 , you should be able to come up with constants that make it fit the definition of
, you should be able to come up with constants that make it fit the definition of 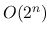 ;
if you think either is not, just explain as best you can why you think it isn't possible to come up with such constants.)
;
if you think either is not, just explain as best you can why you think it isn't possible to come up with such constants.)
This should include the Honor Code pledge, or just the word “pledged”,
plus at least one of the following about
collaboration and help (as many as apply).
Text in italics is explanatory or something for you to
fill in;
you don't need to repeat it!
- I did not get outside help aside from course
materials, including starter code,
readings, sample programs, the instructor.
- I worked with names of other students on this
assignment.
- I got help with this assignment from
source of help -- ACM
tutoring, another student in the course, etc.
(Here, “help” means significant help,
beyond a little assistance with tools or compiler errors.)
- I got help from outside source --
a book other than the textbook (give title and author),
a Web site (give its URL), etc..
(Here too, you only need to mention significant help --
you don't need to tell me that you
looked up an error message on the Web, but if you found
an algorithm or a code sketch, tell me about that.)
- I provided help to names of students on this
assignment.
(And here too, you only need to tell me about
significant help.)
This should be a brief essay
(a sentence or two is fine, though you can write as much as you like)
telling me what if anything you think
you learned from the assignment,
and what if anything you found
interesting, difficult, or otherwise noteworthy.
2022-10-10