CSCI 3323 (Principles of Operating Systems), Fall 2011:
Homework 4
- Credit:
- 40 points.
Be sure you have read Chapter 3, sections 3.1 through 3.3.
Answer the following questions. You may write out your answers by
hand or using a word processor or other program, but please submit
hard copy, either in class or in my mailbox in the department office.
- (5 points)
Consider a computer system with 10,000 bytes of memory
whose MMU uses the simple base register / limit register scheme
described in section 3.2 of the textbook,
and suppose memory is currently allocated as follows:
- Locations 0-1999 are reserved for use by the
operating system.
- Process
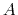 occupies locations 5000-6999.
occupies locations 5000-6999.
- Process
 occupies locations 7000-8999.
occupies locations 7000-8999.
- Other locations are free.
Answer the following questions about this system.
- What value would need to be loaded into the base
register if we performed a context switch
to restart process
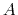 ?
?
- What memory locations would correspond to
the following virtual (program)
addresses in process
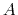 ?
?
- (5 points)
Consider a computer system using paging to manage
memory; suppose it has 64K (
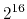 ) bytes of
memory and a page size of 4K bytes, and
suppose the page table for some process (call it process
) bytes of
memory and a page size of 4K bytes, and
suppose the page table for some process (call it process 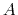 )
looks like the following.
)
looks like the following.
| Page number |
Present/absent bit |
Page frame number |
| 0 |
1 |
5 |
| 1 |
1 |
6 |
| 2 |
1 |
2 |
| 3 |
0 |
? |
| 4 |
0 |
? |
| 5 |
1 |
7 |
| 6 |
0 |
? |
| ... |
0 |
? |
| 15 |
0 |
? |
Answer the following questions about this system.
- How many bits are required to represent a physical
address (memory location) on this system?
If each process has a maximum address space of
64K bytes, how many bits are required to
represent a virtual (program) address?
- What memory locations would correspond to the
following virtual (program) addresses for process
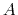 ?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way!)
?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way!)
- 0x1420
- 0x2ff0
- 0x4008
- 0x0010
- If we want to guarantee that this system could
support 16 concurrent processes and give each
an address space of 64K bytes, how much disk
space would be required for storing out-of-memory
pages? Explain your answer (i.e., show/explain how
you calculated it).
Assume that the first page frame is always
in use by the operating system and will never be
paged out. You may want to make additional assumptions;
if you do, say what they are.
- (5 points)
Now consider a bigger computer system,
one in which addresses (both physical and virtual) are 32 bits
and the system has
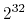 bytes of memory.
Answer the following questions about this system.
(You can express your answers in terms of powers of 2,
if that is convenient.)
bytes of memory.
Answer the following questions about this system.
(You can express your answers in terms of powers of 2,
if that is convenient.)
- What is the maximum size in bytes of a process's address
space on this system?
- Is there a logical
limit to how much main memory this system
can make use of? That is, could we buy and install
as much more memory as we like, assuming no hardware
constraints? (Assume that the sizes of physical
and virtual addresses don't change.)
- If page size is 4K (
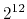 ) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
- Suppose instead the system uses a single inverted page table
(as described in section 3.3.4 of the textbook),
in which each entry consists of
a page number, a process ID,
and four additional bits (free/in-use, referenced,
modified, and read-only), and at most
64 processes are allowed.
How much space is needed for this
inverted page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
How does this compare to the amount of space
needed for 64 regular page tables?
- (5 points)
Tanenbaum says, in one of the questions at the end of
the chapter, that although the 8086 processor provided
no support for virtual memory, there were companies that
sold computer systems that used an unmodified 8086 processor
and did paging. How do you think they managed this?
(Hint: Think about the logical location of the MMU.)
- (5 points)
The operating system designers at Acme Computer
Company have been asked to think of a way of reducing
the amount of disk space needed for paging.
One person proposes never saving pages that
only contain program code, but simply paging them in
directly from the file containing the executable.
Will this work always, never, or sometimes?
If ``sometimes'', when will it work and when will it not?
(Hint: Search your recollections of CSCI 2321 --
or another source -- for a definition of ``self-modifying
code''.)
- (5 points)
How long it takes to access all elements of a large data
structure can depend on whether
they're accessed in contiguous order (i.e., one after another in the
order in which they're stored in memory), or in some other order.
The classic example is a 2D array, in which performance of
nested loops such as
for (int r = 0; r < ROWS; ++r)
for (int c = 0; c < COLS; ++c)
array[r][c] = foo(r,c);
can change drastically for a large array if the order
of the loops is reversed.
Give an explanation for this
phenomenon based on what you have learned from our discussion
of memory management.
For extra credit, give another explanation that is actually
probably likelier to be true of current systems.
Do the following programming problems. You will end up with at
least one code file per problem.
Submit your program source (and any other needed files)
by sending mail to
bmassing@cs.trinity.edu,
with each file as an attachment.
Please use a subject line that mentions the course number and
the assignment (e.g., ``csci 3323 homework 4'').
You can develop your programs on any system that provides the
needed functionality, but I will test them on one of the department's
Linux machines, so you should probably make sure they work
in that environment before turning them in.
- (10 points)
Write a program or programs to demonstrate the phenomenon
described in problem 6.
Turn in your program(s) and output showing differences in execution time.
(It's probably simplest
to just put this output in a text file and send that together with
your source code file(s).)
Try to do this in a way that shows a non-trivial difference in
execution time (so you will likely need to make the arrays or other data
structures large).
I'd prefer programs in C, C++, or Java,
but anything that can be compiled and executed on one of the Linux lab
machines is fine, as long as you tell me how to compile and execute
what you turn in, if it's not C/C++ or Java.
You don't have to develop and run your programs on one of the lab
machines, but if you don't, (1) tell me what system you used
instead, and (2) be sure your programs at least compile and run
on one of the lab machines, even if they don't necessarily give
the same timing results as on the system you used.
Possibly helpful hints:
- An easy way to measure how long program mypgm takes
on a Linux system is to run it by typing time mypgm.
Another way is to run it with /usr/bin/time mypgm.
(This gives more/different
information -- try it.)
If you'd rather put something in the program itself to
collect and print timing information, for C/C++
programs you could use the function in
timer.h
to obtain starting and ending times for the section of
the code you want to time, or for Java programs you could use
System.currentTimeMillis.
- Your program doesn't have to use a 2D array (you might be
able to think of some other data structure that produces
the same result). If you do use a 2D array, though,
keep in mind the following:
- To the best of my knowledge, C and C++ allocate
local variables on the stack, which may be
limited in size. Dynamically allocated variables
(i.e., those allocated with
malloc or new) aren't subject to this limit.
- Dynamic allocation of 2D arrays in C is full of pitfalls.
It may be easier to just allocate a 1D array and fake
accessing it as a 2D array (e.g., the element in
x[i][j], if x is a 2D array, is at
offset i*ncols+j).
Berna Massingill
2011-10-21
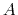 occupies locations 5000-6999.
occupies locations 5000-6999.
 occupies locations 7000-8999.
occupies locations 7000-8999.
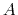 ?
?
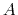 ?
?
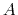 ?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way!)
?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way!)
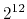 ) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)