CSCI 4320 (Principles of Operating Systems), Fall 2006:
Homework 3
- Assigned:
- October 28, 2006.
- Due:
- November 6, 2006, at 5pm.
- Credit:
- 70 points.
Be sure you have read chapters 3 and 4.
Answer the following questions. You may write out your answers by
hand or using a word processor or other program, but please submit
hard copy, either in class or in my mailbox in the department office.
- (5 points)
Suppose you are designing an electronic funds transfer system,
in which there will be many identical processes that work as
follows:
Each process accepts as input an amount of money to transfer,
the account to be credited, and the account to be debited.
It then locks both accounts (one at a time), transfers the
money, and releases the locks when done. Many of these
processes could be running at the same time.
Clearly a design goal for this system is that two transfers
that affect the same account should not take place at the
same time, since that might lead to race conditions.
However, no problems should arise from doing a transfer
from, say, account
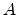 to account
to account  at the same time as
a transfer from account
at the same time as
a transfer from account 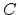 to account
to account 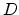 , so another design
goal is for this to be possible.
The available locking mechanism is fairly primitive:
It acquires locks one at a time, and there is no provision
for testing a lock to find out whether it is available
(you must simply attempt to acquire it, and wait if it's
not available).
A friend proposes a simple scheme for locking the accounts:
First lock the account to be credited; then lock the account
to be debited. Can this scheme lead to deadlock?
If you think it cannot, briefly explain why not. If you think
it can, first give an example of a possible deadlock situation,
and then design a scheme that avoids deadlocks, meets the
stated design goals, and uses only the locking mechanism
just described.
, so another design
goal is for this to be possible.
The available locking mechanism is fairly primitive:
It acquires locks one at a time, and there is no provision
for testing a lock to find out whether it is available
(you must simply attempt to acquire it, and wait if it's
not available).
A friend proposes a simple scheme for locking the accounts:
First lock the account to be credited; then lock the account
to be debited. Can this scheme lead to deadlock?
If you think it cannot, briefly explain why not. If you think
it can, first give an example of a possible deadlock situation,
and then design a scheme that avoids deadlocks, meets the
stated design goals, and uses only the locking mechanism
just described.
- (5 points)
Consider a computer system with 10,000 bytes of memory
whose MMU uses the simple
base register / limit register scheme
described in chapter 1 of the textbook
(pages 26-27), and suppose memory is currently allocated
as follows:
- Locations 0-1999 are reserved for use by the
operating system.
- Process
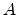 occupies locations 4000-5999.
occupies locations 4000-5999.
- Process
 occupies locations 6000-8999.
occupies locations 6000-8999.
- Other locations are free.
Answer the following questions about this system.
- What value would need to be loaded into the base
register if we performed a context switch
to restart process
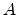 ?
?
- What memory locations would correspond to
the following virtual (program) addresses in process
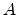 ?
?
- (5 points)
Answer question 9 on p. 264 of the textbook.
Tanenbaum says, in one of the questions at the end of
the chapter, that although the 8086 processor provided
no support for virtual memory, there were companies that
sold computer systems that used an unmodified 8086 processor
and did paging. How do you think they managed this?
(Hint: Think about the logical location of the MMU.)
- (5 points)
Now consider a computer system using paging to manage
memory; suppose it has 64K (
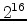 ) bytes of
memory and a page size of 4K bytes, and
suppose the page table for some process (call it process
) bytes of
memory and a page size of 4K bytes, and
suppose the page table for some process (call it process 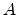 )
looks like the following.
)
looks like the following.
| Page number |
Present/absent bit |
Page frame number |
| 0 |
1 |
4 |
| 1 |
1 |
5 |
| 2 |
1 |
2 |
| 3 |
0 |
? |
| 4 |
0 |
? |
| 5 |
1 |
7 |
| 6 |
0 |
? |
| ... |
0 |
? |
| 15 |
0 |
? |
Answer the following questions about this system.
- How many bits are required to represent a physical
address (memory location) on this system?
If each process has a maximum address space of
64K bytes, how many bits are required to
represent a virtual (program) address?
- What memory locations would correspond to the
following virtual (program) addresses for process
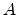 ?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way.)
?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way.)
- 0x1420
- 0x2ff0
- 0x4008
- 0x0010
- If we want to guarantee that this system could
support 16 concurrent processes and give each
an address space of 64K bytes, how much disk
space would be required for storing out-of-memory
pages? Justify your answer.
(If your answer depends on making additional
assumptions, state what they are -- e.g.,
you might assume that
the operating system will always
use the first page frame of memory and will never
be paged out.)
- (10 points)
Now consider a much bigger computer system,
one in which addresses (both physical and virtual) are 32 bits
and the system has
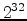 bytes of memory.
(You can express your answers in terms of powers of 2,
if that is convenient.)
Answer the following questions about this system.
bytes of memory.
(You can express your answers in terms of powers of 2,
if that is convenient.)
Answer the following questions about this system.
- What is the maximum size in bytes of a process's address
space on this system?
- Is there a logical
limit to how much main memory this system
can make use of? That is, could we buy and install
as much more memory as we like, assuming no hardware
constraints? (Assume that the sizes of physical
and virtual addresses don't change.)
- If page size is 4K (
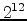 ) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
- Suppose instead the system uses a single inverted page table
(as described in chapter 4, pages 213-214),
in which each entry consists of
a page number, a process ID,
and four additional bits (free/in-use, referenced,
modified, and read-only), and at most
64 processes are allowed.
How much space is needed for this
inverted page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
How does this compare to the amount of space
needed for 64 regular page tables?
- (10 points)
Consider a small computer system with only four page frames
and address spaces consisting of eight pages.
Suppose we start out with all page frames empty
(pure demand paging) and run a program that references
pages in the following order:
(That is, its first reference to memory is in page number 0,
its second reference to memory is in page number 1, etc.)
Compute the number of page faults that occur
during execution of this program if FIFO
page replacement is used, and again if LRU page
replacement is used. (Assume it is possible to implement
LRU perfectly, so the page that is replaced really is the
one least recently used.)
- (5 points)
Consider another small computer system with only four
page frames. Suppose you have implemented the aging
algorithm for page replacement, using 4-bit counters
and updating the counters after every clock tick,
and suppose the
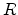 bits for the four pages are as
follows after the first four clock ticks.
bits for the four pages are as
follows after the first four clock ticks.
| Time |
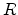 bit (page 0)
bit (page 0) |
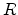 bit (page 1)
bit (page 1) |
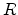 bit (page 2)
bit (page 2) |
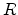 bit (page 3)
bit (page 3) |
| after tick 1 |
0 |
1 |
1 |
1 |
| after tick 2 |
1 |
0 |
1 |
1 |
| after tick 3 |
1 |
0 |
1 |
0 |
| after tick 4 |
1 |
1 |
0 |
1 |
What are the values of the counters (in binary)
for all pages after these four clock ticks?
If a page needed to be removed at that point,
which page would be chosen for removal?
- (5 points)
The operating system designers at Acme Computer
Company have been asked to think of a way of reducing
the amount of disk space needed for paging.
One person proposes never saving pages that
only contain program code, but simply paging them in
directly from the file containing the executable.
Will this work always, never, or sometimes?
If ``sometimes'', when will it work and when will it not?
(Hint: Search your recollections of CSCI 2321 --
or another source -- for a definition of ``self-modifying
code''.)
- (5 points)
A computer at Acme Company used as a compute server
(i.e., to run batch jobs) is observed to be running slowly
(turnaround times longer than expected).
The system uses demand paging, and there is a separate disk
used exclusively for paging.
The sysadmins are puzzled by the poor performance,
so they decide to monitor the system.
It is discovered that
the CPU is in use about 20% of the time, the paging disk
is in use about 98% of the time, and other disks are in
use about 5% of the time. For each of the following,
say whether it would be likely to increase CPU utilization
and why.
- Installing a faster CPU.
- Installing a larger paging disk.
- Increasing the number of processes (degree of
multiprogramming).
- Decreasing the number of processes (degree of
multiprogramming).
- Installing more main memory.
- Installing a faster paging disk.
- (5 points)
How long it takes to access all elements of a large data
structure can depend on whether
they're accessed in contiguous order (i.e., one after another in the
order in which they're stored in memory), or in some other order.
The classic example is a 2D array, in which performance of
nested loops such as
for (int r = 0; r < ROWS; ++r)
for (int c = 0; c < COLS; ++c)
array[r][c] = foo(r,c);
can change drastically for a large array if the order
of the loops is reversed. Give an explanation for this
phenomenon based on what you have learned from our discussion
of memory management.
For extra credit, give another explanation that might also
be true for a computer such as one of our lab machines.
Do the following programming problems. You will end up with at
least one code file per problem.
Submit your program source (and any other needed files)
by sending mail to
bmassing@cs.trinity.edu,
with each file as an attachment.
Please use a subject line that mentions the course number and
the assignment (e.g., ``csci 4320 homework 3'').
You can develop your programs on any system that provides the
needed functionality, but I will test them on one of the department's
Fedora Core 5 Linux machines, so you should probably make sure they work
in that environment before turning them in.
- (10 points)
Write a program or programs to demonstrate the phenomenon
described in problem 10.
Turn in your program(s) and
output showing differences in execution time. (It's probably simplest
to just put this output in a text file and send that together with
your source code file(s).) I'd prefer programs in C, C++, or Java,
but anything that can be compiled and executed on one of the FC5 lab
machines is fine (as long as you tell me how to compile and execute
what you turn in, if it's not C/C++ or Java).
You don't have to develop and run your programs on one of the FC5
lab
machines, but if you don't, (1) tell me what system you used
instead, and (2) be sure your programs at least compile and run
on one of the lab machines, even if they don't necessarily give
the same timing results as on the system you used.
Possibly helpful hints:
- An easy way to measure how long program mypgm takes
on a Linux system is to run it by typing
time mypgm. Another way is to run it with
/usr/bin/time mypgm. (This gives more/different
information -- try it.)
If you'd rather put something in the program itself to
collect and print timing information, for C/C++
programs you could use
the function in
timer.h
to obtain starting and ending times for the section of
the code you want to time,
or for Java programs you could use
System.currentTimeMillis.
- Your program doesn't have to use a 2D array (you might be
able to think of some other data structure that produces
the same result). If you do use a 2D array, though,
keep in mind the following:
- To the best of my knowledge, C and C++ allocate
local variables on the stack, which may be
limited in size. Dynamically allocated variables
(i.e., those allocated with
malloc or new) aren't subject to this limit.
- Dynamic allocation of 2D arrays in C is full of pitfalls.
It may be easier to just allocate a 1D array and fake
accessing it as a 2D array (e.g., the element in
x[i][j], if x is a 2D array, is at
offset i*ncols+j).
Berna Massingill
2006-10-28
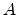 occupies locations 4000-5999.
occupies locations 4000-5999.
 occupies locations 6000-8999.
occupies locations 6000-8999.
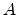 ?
?
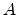 ?
?
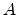 ?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way.)
?
(Here, the addresses will be given in
hexadecimal, i.e., base 16, to make the needed
calculations simpler. Your answers should also
be in hexadecimal. Notice that if you find yourself
converting between decimal and hexadecimal,
you are doing the problem the hard way.
Stop and think whether there is an easier way.)
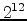 ) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)
) and each page table
entry consists of a page frame number and four
additional bits (present/absent, referenced,
modified, and read-only), how much space is required
for each process's page table?
(You should express the size of each page table
entry in bytes, not bits, assuming 8 bits per byte
and rounding up if necessary.)