Symplectic Maps and Chaotic Dynamics

Mark Lewis

5-7-98

for Chaotic Dynamics

with Dr. Liz Bradley

In the field of chaotic dynamics, numerical integration methods are critical. This is due to the fact that chaotic systems don’t have analytic solutions. For this reason, it is very important to understand the benefits of different integration methods and use the best one accordingly. This paper will examine the properties of a set of methods known as symplectic maps. For some systems and integrations symplectic maps can be far superior to the more standard numerical integration methods.

Symplectic maps should be used to solve Hamiltonian systems, that is any system whose evolution is described by the canonical equations. To understand Hamiltonian dynamics, we should start with a look at Lagrangian dynamics. The Lagrangian of a system is given by where T is the kinetic energy, U is the potential energy, q is the state vector of the system, and the dot denotes a time derivative (Marion and Thornton, 1988). How we can use this function to determine the evolution of the system is given by Hamilton’s principle, which states that the system will evolve in such a way as to minimize the integral of the Lagrangian over the path. Stated in the terms of the calculus of variation:

The path then can be found by applying Euler’s equations:

,

for j=1, 2, …, n, where n is the dimension of the system. This results in n second order differential equations that describe the motion of the system. These equations produce the same results as applying Newton’s laws to the system. However, in many situations, it is easier to find the solution by applying the Lagrangian formalism. This is largely due to the fact that you can pick your choice of position variables, q_i, to use. By selecting the right position variables it is possible to make the differential equations much simpler.

The Hamiltonian formalism can be derived from the Lagrangian and, as it must, it produces the same results as the Newtonian method. However, it also has advantages of its own. These advantages will be more fully illustrated in section 3. Now we will look at exactly what the Hamiltonian formalism is. While Lagrange’s equations of motion used generalized positions and their time derivatives, the Hamiltonian equations use generalized positions and momenta. The generalized momenta are defined by the equation:

.

We then define a quantity known as the Hamiltonian by . With these two definitions, the equations of motion for a system are given by:

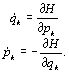(1)

These are often called the canonical equations of motion, and the description of motion that they give is called Hamiltonian dynamics.

As long as H is not an explicit function of time, its value is constant. These are the types of systems that will be generally considered in this paper. In the Lagrangian formalism, we found n second order differential equations. In the Hamiltonian formalism we get 2n first order equations. Where the power of the Hamiltonian formalism arises is in the use of a class of transformations called canonical transformations. When transformed to the proper coordinates, we can get some of those equations to disappear completely and have the remaining ones be trivial to solve. I will talk more about canonical transformations in section 3 where we deal with them more.

When using a normal integration scheme to calculate the trajectory of a Hamiltonian system, the value of H is not conserved. In fact, because such methods tend to systematically add or remove energy from the system, their long term behavior is nothing like that of the true system. Symplectic methods are designed explicitly to conserve the Hamiltonian. Actually, symplectic methods are designed to conserve all of the Poincaré invariants (Channell and Scovel, 1990). The first Poincaré invariant is: , where S indicates that the integral is to be taken over any arbitrary 2-surface in phase space (Goldstein, 1965). We can define n such invariants by extending this to , where now the integrals are taken over a 2n-dimensional surface. A corollary of conserving the Poincaré invariants is that Liouville’s theorem is also valid in the mapped system. That theorem states that volumes of phase space are conserved over time evolution, and as a result of this, the energy of the system (or the Hamiltonian) is also conserved.

The reason why symplectic maps conserve all of these quantities because they actually solve a Hamiltonian exactly. Granted, it is not necessarily the Hamiltonian that one is interested in, but it is similar. An example of this will be given in the next section. For this reason, symplectic methods are very well suited for integrations of conservative systems in which there are a wide range of time scales and hence a large number of time steps must be taken.

2. Simple Symplectic Maps

We have seen that symplectic methods have some nice properties for certain types of integrations. However, the question still remains of how one finds a symplectic map, and if we did, how would we know? The second question is rather easy to answer: a mapping is symplectic if

, (2)

where L is the Jacobian matrix of the mapping, and . The first question has no generally valid, easy answer. If one is willing to place certain restrictions on the types of problems that he or she is looking at, then some reasonably simple methods can be devised.

One assumption that greatly simplifies the derivation of the mapping without losing too much generality in real world applications is to assume that the Hamiltonian can be expressed as:

, (3)

(Yoshida, 1992), where often T is the kinetic energy and V is the potential energy. Typically, any physical system that doesn’t include friction will have a Hamiltonian of this form. Let’s look at one of the simplest systems for an example, the simple harmonic oscillator (SHO). By choosing proper mass and spring constants, the Hamiltonian for the SHO can be written as:

. (4)

Plugging this into the canonical equations (1) produces the system of equations:

If we plug these equations into Euler’s method, the resulting map has the form:

.

This mapping is not symplectic, which can be easily seen by looking at how the value of the Hamiltonian (4) changes with each iteration: . Luckily it can be easily modified to be symplectic. The altered map:

is exactly symplectic. We can show this using the symplectic condition (2) given at the beginning of this section:

.

With a little algebra one can easily see, however, that this mapping does not conserve (4) under iteration. This is because, as mentioned earlier, symplectic maps solve some Hamiltonian exactly, but not the exact one that we are interested in. In the case of this mapping, the quantity that is conserved exactly is:

(5)

So we have found a symplectic integrator for the SHO, but it really isn’t of much value other than as an example because the SHO has a rather simple analytic solution. In order to deal with other systems, we still need a general method for finding solutions to Hamiltonians of the form (3). A general, first order symplectic map of this form is given by the equations

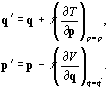(6)

This mapping is actually made up of two composed symplectic maps. The first is (q,p)® (q’,p), and the second is (q’,p)® (q’,p’). By playing with (2), we can easily show that the composition of any two symplectic maps produces a symplectic map. Assume that K and L are two symplectic maps, then:

.

Like with the SHO example, the mapping produced by (6) solves some alternate Hamiltonian exactly. Yoshida (1992) proved that this alternate Hamiltonian is given by , where . Here the subscripted p’s and q’s denote partial derivatives with respect to those variables. Notice that applying this to (4) produces (5) as it should.

This is great if you don’t mind forever doing first order calculations (which isn’t nearly as bad with symplectic methods as it is with normal methods), but generally this isn’t the case. Once again dealing with Hamiltonians of the form (3), one can find a symplectic integrator of order k of the form:

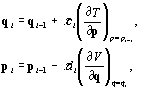(7)

where iÎ [1,k]. For the first order method we found the coefficients to be c₁=d₁=1. For a second order method they are c₁=c₂=1/2, d₁=0, d₂=0. Forest and Ruth (1990) derived a fourth order method with the result that

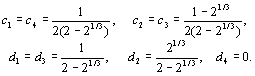
All three of these methods are implemented in the Java applet so that you can compare how they perform under different circumstances.

3. Special Symplectic Maps

While the above methods are simple to derive and work on a relatively large subset of Hamiltonian systems, they run at about the same speed as normal methods of the same order, and hence can make the long term integrations where they are of most value impossible or prohibitively expensive. To overcome this, we can sacrifice the flexibility of these methods and instead derive faster methods that only work on very specific types of systems. There are about as many ways to do this as there are authors writing on the topic and doing any of them properly is something of a black art. However, two methods stand out as being significant (Hadjidemetriou, 1996). Optimized methods are most easily derived when one can break the Hamiltonian of the system into pieces that can be dealt with more efficiently. For the discussion here, this means splitting it into a dominating piece that is integrable and a much smaller piece which isn’t necessarily integrable, H=H₀+e H₁.

Before going into a description of these methods, we need some more knowledge and another set of tools. In the first section I mentioned that there are advantages to using the Hamiltonian formalism because of the use of canonical transformations. A canonical transformation is one that alters the coordinates and Hamiltonian of the system in such a way that the canonical equations, (1), still describe the motions of the system. There are four types of canonical transformations that transform from (q,p) to (Q,P) and each one has associated with it a generating function (Lichtenberg and Lieberman, 1983). Canonical transformations of the first kind use a generating function F₁, which is a function of q, Q, and t. One finds that with this function:

(8)

(9)

and

. (10)

One can then define other generating functions in terms of one old and one new variable by way of Legendre transforms. For example, defines the generating function of the second kind, and with this generating function, the other variables and the Hamiltonian are given by

(11)

(12)

and

. (13)

Similar sets exist for the third and fourth types of generating functions, which use the old momenta with new positions and the old momenta with new momenta respectively.

One might find the ability to transform from one coordinate system to another useful for trying to uncover underlying properties of a system if for nothing else. However, the power of canonical transformations is actually much greater. In section 1, I mentioned that we could use these transformations to reduce the number of differential equations we needed to solve. Finding what are known as action-angle coordinates accomplishes this. For every conserved quantity in the system, a momentum-position pair can be transformed into action-angle coordinates. They are generally denoted as I for the action, and q for the angle. In those coordinates, the angle (or position) doesn’t explicitly appear in the Hamiltonian. Because of this, the associated momentum is a constant, which implies that the evolution of that coordinate is linear in time. The coordinates that don’t appear in the Hamiltonian are often called cyclic coordinates. It also turns out that mappings of Hamiltonian systems are derivable as canonical transformations. This property will be used in the second method discussed

The first method that I will discuss here uses a technique called averaging. When e =0, the system is completely integrable, and as such can be solved exactly. If we wished, we could transform all of the coordinates to action-angle coordinates. In that coordinate system, the Hamiltonian is of the form H=H₀(I)+H_F(I,q ), and we can represent H_F as a Fourier series. Because the non-integrable piece is much smaller, one can apply perturbation theory’s method of averaging to this series. This leads to an averaged Hamiltonian that looks like , where the bars signify averaged quantities. This process averages out the high frequency terms in the perturbation. By introducing a different (more manageable) set of high frequency terms, the angle dependence can be changed into a periodic delta function. This type of system is then easy to solve, because you first solve for the evolution of the system under H₀, then at periodic intervals you solve for the effects of the delta function.

This type of method is commonly used in planetary science where the motion of bodies is dominated by the gravitational attraction of the Sun. The integrable piece of the Hamiltonian is just Keplarian motion while the perturbation is the gravitational interactions of the various bodies. Jack Wisdom (1983) first used this type of method to examine the long-term motions of particles in the asteroid belt in certain resonances. Those codes were very limited in their flexibility as they had to be explicitly written to consider different resonances. Later Wisdom and Holman (1991) developed a much more general method that works for orbits in any system that is dominated by a central mass, assuming that there are no close encounters. This method is know as the Multi-Variable Symplectic (MVS) method because it uses three different coordinate systems.

There is one serious drawback to the averaging method. It isn’t guaranteed to produce a symplectic mapping (Hadjidemetriou, 1996). In the case of the MVS method, the mapping ceases to be symplectic when close encounters occur. This is largely due to the fact that the derivation assumes that the integrable piece of the Hamiltonian dominates. For the MVS method, this is equal to assuming that the motion is dominated by the central mass. When a close encounter occurs, this assumption fails, and hence the integration method breaks down. For the case of a map derived by averaging, this breakdown often implies that the map becomes non-symplectic.

Another method of finding a symplectic map is to once again begin with the Hamiltonian in the action-angle coordinates of its integrable part. Once in this form, it is simple to find a mapping for the Poincaré section of the integrable part as a canonical transform. This mapping is associated with a generating function of the second kind, as described by (11), (12), and (13), by the equations:

. (14)

We then add a perturbation to this generating function. Hadjidemetriou (1991, 1993) proved that the proper perturbation is given by the perturbation of the averaged Hamiltonian multiplied by 2p . Applying (14) to the new perturbed generating function results in the symplectic map of the system.

According to Hadjidemetriou (1996), this method produces a mapping that is always symplectic and also has the same fixed points as the original system. Those fixed points have the same stability characteristics as the original system. This is of significance, because it leads one strongly to believe that the systems described by the mapping and by the original Hamiltonian, will have very similar characteristics. This is good because that was part of the goal in using a symplectic map in the first place.

4. Integrating Chaotic Systems

Now let’s go back to the simple mappings that were derived in section 2, as those are the methods that have been implemented in the Java applet (as well as first, second, and fourth order Runga-Kutta algorithms). The code is written so that different methods can easily be interfaced with different systems. The same base classes are also used for analyzing the changes in the KAM tori as described in the next section.

One of the first things that can be tested with this code is at what value of the time step the energy conserving nature of the integration method breaks down. For the SHO, this occurs below a value of 0.03 for the Euler method, around 0.1 for the second order Runga-Kutta, and around 0.4 for the fourth order Runga-Kutta. For the symplectic methods, the point of breakdown occurred at much larger values. As the time step is increased, the oscillations in the energy grow in amplitude, but the average value remains near the true value. This behavior continued until the time step was on the order of the oscillation period of the pendulum for the first and second order symplectic methods. Oddly, the fourth order method experienced catastrophic breakdown at a smaller value of 0.8. One big advantage of this is that if you are primarily concerned with the qualitative behavior of the system than the exact placement of particles then large time steps can be used with the symplectic methods. In the study of chaotic dynamics, the qualitative behavior is often all that really matters anyway because the sensitive dependence on initial circumstances tends to make the exact position and velocity values somewhat meaningless.

If you look back at the coefficients for equation (7) in section 2 you will notice that . It is interesting to note here that the first time I entered the numerical values for the fourth order mapping, I did something very wrong, and they were completely erroneous, to the point that their sums weren’t equal to 1. What was interesting about this was that the mapping was still symplectic even though it most definitely wasn’t fourth order (in fact its solution was far worse than first order). There were very large oscillations in the energy of the system, but it remained bound within a certain region around the actual energy of the system. Upon deeper contemplation, this behavior isn’t at all odd. Remember that these maps are composed of a number of symplectic maps such as (q,p)® (q’,p) in the first order system. The symplectic nature of this mapping didn’t depend on the coefficients, it only requires that the Hamiltonian has the form given in equation (3).

When working on the program for the next section, looking at KAM tori, I learned that in order for the methods given in section 2 to work, the Hamiltonian must truly be separable in q and p. If this condition is not met, the resulting maps not only fail to be symplectic, but they fail to be accurate maps of the system at all. This is not unlike the condition on the MVS method that the gravitational force of the Sun be more important than that from other bodies in the system. It is possible to conceive of a system where the form of the Hamiltonian was something like

.

This system would work well with the methods from section 2 as long as the two epsilon values were small. As soon as they grew too large, the mapping would lose both its symplectic nature, and its accuracy.

There is one more significant fact to consider when using symplectic methods to integrate systems: a method ceases to be symplectic if you vary the time step. With standard methods it is common to create adaptive algorithms that vary their time step depending on the dynamics of the region of phase space the system is currently in. The reason that is not acceptable with symplectic methods is that the value of the Hamiltonian tends to oscillate as the system evolves. When the time step is changed, the current value of H essentially becomes the "base" value for the evolution with the new time step. Hence changing time steps in symplectic methods causes them to lose their symplectic nature. One could argue that there would tend to be zero net movement in the Hamiltonian because it is just as likely to be in down half of the oscillation as it is in the up. However, this argument doesn’t really hold true, because the changes in time step tend to happen in similar regions of phase space, at systematic time intervals. For this reason it is likely that if the time step is changed at a high point in the oscillation once then the same type of change in time step will happen again at another high point.

This does not mean that all hope is lost for coming up with adaptive symplectic methods. Instead of changing the t value being used, adaptive symplectic methods essentially change their accuracy. Remember that the composition of symplectic maps results in a symplectic map. When the system moves into a region that would normally require smaller time steps, the current time step is instead broken down into a larger number of "small" symplectic maps. An example of an adaptive, symplectic method was recently developed by Duncan, Levison, and Lee (1997). The method is called the Symplectic Massive Body Algorithm (SyMBA) and is intended to replace the MVS method, especially in systems where close encounters are important. This method essentially treats the regions around the smaller bodies like an onion and uses a different mapping for each layer. When a close encounter occurs, all of the mappings for the layers that the visiting particle passes through are composed to form a valid mapping for the entire time step during the encounter.

Altering KAM Tori

My first idea was to see if the behavior of the system could be altered away from integrability just by increasing the step size when e =0. This doesn’t work at all, because without the perturbations, the solution is linear. In fact, that system is solved exactly by any of the methods in the applet, including the standard Euler’s method. So the alterations due to symplectic methods can’t break down any of the tori alone, there must be some perturbation.

After realizing this, I started to play with different value of epsilon to see if I could find regions where the tori were breaking down in general. These were easy to find just by bumping e to 0.01 or so. At that point a number of island chains begin to break off. This gave me hope that what I was plotting was something close to what I wanted to be plotting. Then I returned to seeing how the magnitude of the time step might effect the presence of these islands. It turns out that doing such a search isn’t actually all that easy, but eventually I found what I was looking for. Using the second order symplectic method at a certain distance from the origin (this distance is the first action, p₁), there was a single slightly misshapen ring when the time step was equal to 1. When I boosted it up to 2, there was a separatrix between three islands instead of the single torus. The breakdown of that particular torus appeared to begin around the time that the time step was 1.5.

This result leads me to conclude that it is possible for the changes that result from using a symplectic map to alter the global structure of the behavior of the system. However, this only happened in a visible or appreciable way when the time steps were much larger than anyone should generally set them. Therefore, they seem rather safe to use as long as the time step of the system is set to a reasonable value.

When dealing with averaging methods, the situation may not be quite so bright. Just because we are applying a symplectic map, the effective Hamiltonian is going to be altered. However, another alteration was introduced in the averaging process. Even worse, unlike the simple methods from section 2, the amount of difference between the true Hamiltonian and the one solved by the mapping varies with the state of the system. The larger the value of e in front of H₁, the further apart these two systems will be. I should note here that I didn’t actually run any of these averaging methods to test my instincts on this and hence my predictions should be taking with a grain of salt.

6. Conclusions

If you ever need to integrate a specific Hamiltonian system for any significant period of time, I would recommend, based on what I have found, that you use a symplectic method. They are much more stable and accurate over long periods of time than standard methods. Also, though they are somewhat harder to derive, if the derivation is done properly, the speed of the integration can be greatly enhanced. Though these methods actually solve a different Hamiltonian than the one we are interested in, it doesn’t appear that under normal circumstances that the Hamiltonian is altered to a great enough degree to change the behavior of the system.

There is definitely more work that could be done in this topic. I never did manage to implement and experiment with measuring the Lyapunov exponents as generated by different methods. The first applet that I wrote does measure the Lyapunov exponent, but I was never fully convinced that I ever found parameters for which the measured value was actually greater than zero.. However, I think that it seems like a safe assumption that those associated with the symplectic maps will tend to be the most reliable simply due to the long term evolution in systems being integrated with standard methods. Also, because the sign of the exponents is all that really matters in most situations it won’t matter if the results from a method differ from exact in the second or third decimal place.

Bibliography