![]()
![]()
This article proposes a consistent hedge-effectiveness measurement scheme for hedge accounting under Financial Accounting Statement (FAS) 133 and International Accounting Statement (IAS) 39. More specifically, it derives a consistent deferral accounting calculation scheme based on what the Financial Accounting Standards Board and the International Accounting Standards Committee had originally wanted to propose as a hedge-effectiveness measuring mechanism, using history as our best guide to the future.
You will see that Infinity HedgeCORRect™ as a statistical (correlation) approach to measuring hedge effectiveness has the following advantages:
In short, our proposal is:
Firstly, neither Statement specifies a method for effectiveness testing. According to paragraph 62 of FAS 133, "This Statement does not specify a single method for either assessing whether a hedge is expected to be highly effective or measuring hedge ineffectiveness." Similarly, paragraph 151 of IAS 39 states that "[t]his Statement does not specify a single method for assessing hedge ineffectiveness." However, FAS 133 does provide examples of assessing effectiveness by comparing historical PVs and by measuring forecasted correlations. Even in the given examples, the ineffectiveness calculation used to drive accounting entries is based on the chosen method of measurement. Clearly, the Statement has made a deliberate effort to allow room for different methods to be applied. In addition, the Statement provides specific criteria of when effectiveness testing may be by-passed altogether: such as by matching principal amounts, indices, reset dates, embedded options, maturity date, and commodity delivery points.
Secondly, once the user decides on a particular method of testing, the results are applied rather differently toward deferral accounting for cashflow hedges as opposed to fair-value hedges. In the case of cashflow hedges, deferral accounting can be applied up to the effective amount, but overhedging must be recognized up-front. In the case of fair-value hedges, all P/L variations due to any ineffectively hedged amounts must be recognized in the current period.
Thirdly, paragraph 62 of FAS 133 requires the "consistent application of a defined method" both a) at inception and on an on-going basis for measuring expected effectiveness and b) for measuring the ineffective part of the hedge. Likewise, paragraph 147 of IAS 39 states that "[t]he method an enterprise adopts for assessing hedge effectiveness will depend on its risk management strategy." The key concept introduced by both Statements is consistency with respect to the entity’s risk management strategy. Any change of measurement method will need to be justified and the trade-to-hedge relationship will need to be designated anew. Moreover, "an entity should assess effectiveness for similar hedges in a similar manner; use of different methods for similar hedges should be justified."
We understand that the Discussion Paper (jointly developed by the IASC and a number of national standard setters) and the Exposure Drafts (the FASB and IASC each had their own version) originally intended to prescribe a hedge effectiveness test. The test was thought to be a straightforward measurement of the statistical correlation between the hedge and the hedged portfolio. Subsequently, such a position was reversed due to controversies over the difficulty of implementing such a measure and the lack of consensus over a "proper" measure of correlation. Since observed correlations are known to break down during volatile market circumstances, such a scheme can be seen as imposing artificial constraints on hedgers by encouraging hedges that may be biased in favor of accounting treatments instead of hedging economics. Furthermore, the fact that a hedge and its hedged portfolio may be highly correlated statistically does not necessarily immunize the portfolio from unexpected large PV fluctuations that the Statements intend hedging entities to recognize in earnings. Finally, correlation is a linear measure that does not capture higher-order effects introduced by optionality.
To proceed, we will borrow a paradigm used by Professor David Health in his discourse on a coherent risk measure. If a certain measure is not good enough, is it possible to improve it in a way that preserves the regulators’ original intent? Clearly, we are not in the business of inventing new regulations. If we were to introduce an alternative approach within the confines allowed by the accounting standards, they should be at least consistent with any existing, acceptable proposal in order to be palatable to regulators. As it turns out, we can translate correlation into an alternative measure with such a property.
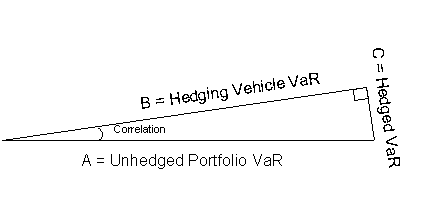
The diagram illustrates the concept by using the geometric notation proposed by Robert Litterman. Suppose A denotes the VaR of the unhedged position and B denotes the VaR of the hedging vehicle, the correlation between A and B is cos(Ð AB). The hedged VaR is the third edge C of the right triangle formed by using A as the hypotenuse. This gives the percentage risk reduction of 1-sin(- AB). Accordingly, we can derive a direct mathematical relationship between the portfolio-to-hedge correlation and the percentage of risk reduction, which is:
![]()
The current guidelines are that the hedge and the portfolio should be at least 80% correlated in order to qualify for hedge accounting, which translates into a minimum of 40% risk reduction. In other words, any hedging vehicle or portfolio of hedging vehicles that can reduce the risk of a portfolio by more than 40% should qualify for hedge accounting. There are tangible advantages of using this alternative measure instead of the statistical portfolio-to-hedge correlation. Statistical correlation is essentially a linear measure whereas the percentage of risk reduction can capture higher-order effects, provided that the appropriate risk measure is applied. For instance, it is recommended that under the dollar-offset (or PV) method the intrinsic value of an option should be used to measure its effectiveness as a hedge. That results in certain conceptual inconsistencies. Indeed, it will be controversial to ascertain the intrinsic value of a barrier option near its knock-out level. Using an appropriate risk measure that can effectively capture second-order effects eliminates this problem.
A leading investment bank has proposed the alternative of using short-term observed historical PVs to calculate correlations by performing a regression test. However, many of the following arguments against using historical PVs to measure "ex-ante" risk – once again, what we are effectively measuring here is residual risk – have been well fleshed out since the early days of modern market-risk management. To put it mildly, we are not strong believers in this alternative approach unless you run into difficulties in obtaining reliable variance/covariance matrices, such as those for emerging markets. A fuller explanation is set out in the following paragraphs:
Cashflow Hedges. We will proceed by illustrating the proposed approach by example before getting into any detailed analysis. Suppose we have a forecasted transaction with an initial value of 2 dollars that is hedged by a 90%-correlated hedge. Next, there is a "blip" on our radar screen, so that the forecasted transaction loses half of its MTM value on Day 91 and bounces back to 2 dollars on Day 183. The earnings impact due to ineffectiveness is illustrated by the "overhedge" example as shown below. The steps involved are straightforward:
D MTM = D OCI + D Earnings
should always hold on a period-by-period basis regardless of how you intend to split the PV variations (D MTM) from your hedge into D OCI and D Earnings.
| DAY 1 | DAY 91 | DAY 183 | |||||
| Forecasted transaction | |||||||
| MTM | USD | 2.000 | 1.000 | 2.000 | |||
| D MTM | USD | 0.000 | -1.000 | 1.000 | |||
| Hedge | |||||||
| MTM | USD | 0.000 | 1.100 | 0.000 | |||
| D MTM | USD | 0.000 | 1.100 | -1.100 | |||
| % Ineffectiveness |
|
| |||||
| D OCI | USD | 0.000 | 1.000 | -1.000 | |||
| D Earnings | USD | 0.000 | 0.100 | -0.100 | |||
| Net Earnings | USD | 0.000 | 0.100 | 0.000 | |||
Note that nothing was said about how to account for the forecasted transaction itself. That depends on the type under consideration:
Another caveat is that a few more "if-then-else" rules as specified by
paragraph 30(b) should be checked before one can recognize these earnings
figures. The paragraph states that overhedging, but not underhedging, should be
recognized. We will illustrate the corresponding treatment for "underhedging" in
the diagram below:
| DAY 1 | DAY 91 | DAY 183 | |||||
| Forecasted transaction | |||||||
| MTM | USD | 2.000 | 1.000 | 2.000 | |||
| D MTM | USD | 0.000 | -1.000 | 1.000 | |||
| Hedge | |||||||
| MTM | USD | 0.000 | 0.900 | 0.000 | |||
| D MTM | USD | 0.000 | 0.900 | -0.900 | |||
| % Ineffectiveness |
|
| |||||
| D OCI | USD | 0.000 | 0.900 | -0.900 | |||
| D Earnings | USD | 0.000 | 0.000 | 0.000 | |||
| Net Earnings | USD | 0.000 | 0.000 | 0.000 | |||
In this case, the PV variation from the hedge falls short of offsetting the PV variation from the hedged item. Thus, the entire PV variation from the hedge can be deferred to OCI. We note that the Board initially considered the approach of deferring the full amount of 1 dollar and reporting a 10 cents deficit in earnings. It subsequently decided against the approach, along with a related decision that the ineffectiveness due to any cashflow hedges should be determined on a cumulative instead of a period-by-period basis. In other words, an underhedge with a 10 cents deficit in this period can be offset against the 10 cents surplus of an overhedge in the next period, so that there should not be any net earnings impact. One convenient way to implement this rule without having to store every single PV across all relevant reporting periods is to keep a "deficit bucket" (as in the alternative approach previously considered by the Board), even though the bucket is not being reported in the actual deferral calculation.
Fair-Value Hedges. The Board originally proposed a symmetrical approach for fair-value hedges by keeping any underhedged amount in an "unrecognized" reserve and recognizing any P/L amounts due to any effectively hedged or overhedged amount. The Board subsequently reversed that position. As a result, there is little difference between the present treatment and MTM accounting in practice. The following table illustrates the accounting treatment for our previous "underhedging" example as a fair-value hedge:
| DAY 1 | DAY 91 | DAY 183 | |||||
| Firm Commitment | |||||||
| MTM | USD | 2.000 | 1.000 | 2.000 | |||
| D MTM | USD | 0.000 | -1.000 | 1.000 | |||
| Hedge | |||||||
| MTM | USD | 0.000 | 0.900 | 0.000 | |||
| D MTM | USD | 0.000 | 0.900 | -0.900 | |||
| % Ineffectiveness |
|
| |||||
| D Earnings | USD | 0.000 | -0.100 | +0.100 | |||
| Net Earnings | USD | 0.000 | -0.100 | 0.000 | |||
To conclude, the following table illustrates the accounting treatment for our previous "overhedging" example as a fair-value hedge:
| DAY 1 | DAY 91 | DAY 183 | |||||
| Firm Commitment | |||||||
| MTM | USD | 2.000 | 1.000 | 2.000 | |||
| D MTM | USD | 0.000 | -1.000 | 1.000 | |||
| Hedge | |||||||
| MTM | USD | 0.000 | 1.100 | 0.000 | |||
| D MTM | USD | 0.000 | 1.100 | -0.100 | |||
| % Ineffectiveness |
|
| |||||
| D Earnings | USD | 0.000 | 0.100 | -0.100 | |||
| Net Earnings | USD | 0.000 | 0.100 | 0.000 | |||
![]()
and the corresponding single-period change in hedge value as
![]() .
.
In other words, we have defined ![]() and
and ![]() as
as
![]() and
and ![]()
The Statement only asks us to choose a certain approach to measure hedge effectiveness and compute an ineffective amount based on the defined approach. The Board’s reluctance to provide indicative quantitative guidance has led to considerable confusion among practitioners. We want to emphasize the importance of choosing a correct approach by demonstrating the problems arising from a percentage ineffectiveness computation based on one "home-baked" flavor of the cumulative dollar-offset (PV) approach that we have come across. This approach leads to a counterintuitive, if not undesirable result, as follows:
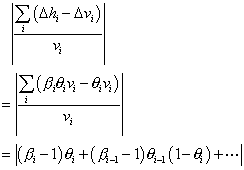
By applying a dictionary interpretation of the Statement to perform a deferral calculation for a cashflow hedge, one can obtain the earnings impact reported in the first period by multiplying the hedge’s single-period P/L to the computed percentage ineffectiveness:

Crudely speaking, ![]() can be seen as a
single-period measure of the i-th period volatility of the underlying
forecasted transaction;
can be seen as a
single-period measure of the i-th period volatility of the underlying
forecasted transaction; ![]() is the
corresponding "volatility-adjusted" measure of the correlation between the
underlying forecasted transaction and the hedge, which carries an expected value
of one if you intend to hedge perfectly. Note that the leading term of our
earnings impact for the i-th period is quadratic in both
is the
corresponding "volatility-adjusted" measure of the correlation between the
underlying forecasted transaction and the hedge, which carries an expected value
of one if you intend to hedge perfectly. Note that the leading term of our
earnings impact for the i-th period is quadratic in both ![]() and
and ![]() . If you take the expected value of the total sum of earnings impacts
across all periods, you are likely to end up with a messy non-zero
expression that bears some resemblance to the dot product of the
variance of
. If you take the expected value of the total sum of earnings impacts
across all periods, you are likely to end up with a messy non-zero
expression that bears some resemblance to the dot product of the
variance of ![]() and
and ![]() even if
you have hedged perfectly in the first place, i.e.
even if
you have hedged perfectly in the first place, i.e. ![]() ! Another
consequence of such quadratic dependence is the convexity effects associated
with Jensen’s inequality. In layman’s terms, you will end up with a net earnings
impact even if there is a "blip" on the radar at the end of the reporting
period, and everything returns to exactly as before on the next day. This is the
counterintuitive, if not undesirable result referred to earlier.
! Another
consequence of such quadratic dependence is the convexity effects associated
with Jensen’s inequality. In layman’s terms, you will end up with a net earnings
impact even if there is a "blip" on the radar at the end of the reporting
period, and everything returns to exactly as before on the next day. This is the
counterintuitive, if not undesirable result referred to earlier.
Next, we repeat the same analysis for the method that the Board originally
intended based on statistical correlations. We start by defining a
quantity ![]() as the expected "volatility-adjusted" correlation between the
underlying forecasted transaction and the hedge. We will simplify the argument
by assuming that
as the expected "volatility-adjusted" correlation between the
underlying forecasted transaction and the hedge. We will simplify the argument
by assuming that ![]() can be effectively
estimated as a known constant. In other words, we assume that
can be effectively
estimated as a known constant. In other words, we assume that ![]() where
where ![]() is the noise term with
is the noise term with ![]() . Ineffectiveness,
as computed by this method, is given by the noise term
. Ineffectiveness,
as computed by this method, is given by the noise term ![]() and the expected
hedge error
and the expected
hedge error ![]() . The earnings
impact reported at the i-th period according to this approach is
. The earnings
impact reported at the i-th period according to this approach is
![]() .
.
Hence, the total sum of earnings impacts across all periods is
![]() .
.
The issue of "cumulative" ineffectiveness can be addressed by keeping a
"deficit bucket", but these implementation details can be omitted without any
material impact on our analysis. The current situation is more in line with our
intuition. If you take the expected value of the total sum of earnings impacts
across all periods, you will arrive at a zero expected value when you
hedge perfectly, i.e. ![]() . Moreover, the
total sum of earnings impact is linear to the dot product of
. Moreover, the
total sum of earnings impact is linear to the dot product of ![]() and
and ![]() . In other words, if the market is more volatile, or if you have chosen
to hedge in a less than perfect manner, the expected impact in this case
increases proportionally instead of quadratically. Notice how the
forecasted correlation cancelled out in the algebra. We have indeed derived a
method for ex-post assessment that is purely based on comparing historical PVs
and is fully consistent with our statistical (correlation) method for ex-ante
assessment. Such a method can be readily applied to many real-world situations.
. In other words, if the market is more volatile, or if you have chosen
to hedge in a less than perfect manner, the expected impact in this case
increases proportionally instead of quadratically. Notice how the
forecasted correlation cancelled out in the algebra. We have indeed derived a
method for ex-post assessment that is purely based on comparing historical PVs
and is fully consistent with our statistical (correlation) method for ex-ante
assessment. Such a method can be readily applied to many real-world situations.
We recall that two error terms (the expected hedge error and the noise term)
were previously accounted for. We thus propose the following paradigm: Assuming
that![]() is an estimable constant over the entire period spanning the trade-to-hedge
relationship, we eliminate all the expected hedge error and defer a just
enough amount to give a zero P/L on average when reversing any
yet-to-be-recognized amount. As long as it can be proven mathematically that the
fair-value of that noise term is zero, it is consistent with Generally-Accepted
Accounting Practice to defer the recognition of a noise term until the error
actually materializes. For instance, expected value is routinely considered to
be the fair-value used in the MTM accounting for yet-to-be exercised
options. Hence, instead of two error terms, it suffices to defer just the
expected hedge error, given that the fair-value of the noise term is zero, as
follows:
is an estimable constant over the entire period spanning the trade-to-hedge
relationship, we eliminate all the expected hedge error and defer a just
enough amount to give a zero P/L on average when reversing any
yet-to-be-recognized amount. As long as it can be proven mathematically that the
fair-value of that noise term is zero, it is consistent with Generally-Accepted
Accounting Practice to defer the recognition of a noise term until the error
actually materializes. For instance, expected value is routinely considered to
be the fair-value used in the MTM accounting for yet-to-be exercised
options. Hence, instead of two error terms, it suffices to defer just the
expected hedge error, given that the fair-value of the noise term is zero, as
follows:
![]()
If you take the expected value of the total sum of earnings impacts across
all periods, you arrive at an estimate that is proportional to the covariance
of ![]() and
and ![]() , i.e. you will have
the expected behavior as long as you hedge correctly, not just perfectly.
It is well known that perfect hedges rarely exist, and that a sound reporting
framework should encourage correct hedging decisions. However, in order
to take advantage of the zero fair value, the hedging entity will need to be
able to calculate an unbiased hedge and separate out the hedge error as
often as correlation changes, such as on a weekly or even daily basis. Infinity
HedgeCORRect™ can perform this computation "on the fly" when measuring
ex-ante hedge effectiveness.
, i.e. you will have
the expected behavior as long as you hedge correctly, not just perfectly.
It is well known that perfect hedges rarely exist, and that a sound reporting
framework should encourage correct hedging decisions. However, in order
to take advantage of the zero fair value, the hedging entity will need to be
able to calculate an unbiased hedge and separate out the hedge error as
often as correlation changes, such as on a weekly or even daily basis. Infinity
HedgeCORRect™ can perform this computation "on the fly" when measuring
ex-ante hedge effectiveness.
There are several practical advantages to this proposition. Firstly, the dollar-offset (PV) approach recognizes both the hedging error and a noise term in earnings. In contrast, the statistical (correlation) approach recognizes only the hedging error and leaves any unrealized noise term at its fair value of zero. Indeed, the former method introduces volatility in earnings that can be seen by some as at best unnecessary. In the extreme case, one can construct accounting scenarios consisting of all noises with negligible hedging errors. An excellent illustration of how a real-life "perfect" hedge can introduce volatility in earnings has been provided Professor Robert Jensen. Secondly, recognizing a zero-mean noise term in earnings may have negative tax consequences, as profits are taxed while losses are not. In a long-term hedging relationship, a profit taxed this year may be offset by a loss accrued next year; but the Statement provides no clear provision on recovering any tax paid. Although this may not be a serious problem for a large trading book in which zero-mean profits and losses are expected to cancel out, it nonetheless introduces an unnecessary bias into the accounting scheme that could have easily been addressed by deferring the correct amount in the first place. Finally, under the dollar-offset (PV) approach, there is no rational mechanism for allocating ineffectiveness to individual hedging trades in a portfolio of hedges as required by the Statement. As for the statistical (correlation) approach, such a problem can be easily addressed since ineffectiveness is simply the position above or below the optimal hedging position. This is consistent with the type of risk and hedging analysis needed by the front office.
A legitimate question arises in the following situation: we have eliminated
the noise term, but at the same time a statistical estimate prone to estimation
errors has also been introduced into our calculation. Have we gained net
accuracy in the process? Suppose the best statistical estimate available for our
desired correlation ![]() is
is ![]() . Hence,
the error given by the statistical (correlation) approach is:
. Hence,
the error given by the statistical (correlation) approach is:
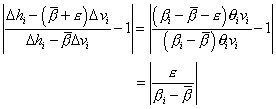
By contrast, the error given by the noise term in the dollar-offset (PV) approach is:
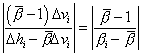
These two expressions allow for easy comparison as they share a common
denominator. As mentioned earlier, perfect hedges rarely exist in real life.
Indeed, the Statement allows the "imperfection" factor of![]() to be as large as
20%. On the other hand, it is possible to obtain reliable variance/covariance
matrix from publicly available sources, bearing in mind that a 5% error would
represent a reasonably conservative error margin. Based on such a crude
analysis, we enjoy a 400% increase in accuracy. The specific gain in accuracy
depends on the quality of the variance/covariance data available for the
specific currencies required. One can expect with reasonable confidence that the
gain will be a significant one.
to be as large as
20%. On the other hand, it is possible to obtain reliable variance/covariance
matrix from publicly available sources, bearing in mind that a 5% error would
represent a reasonably conservative error margin. Based on such a crude
analysis, we enjoy a 400% increase in accuracy. The specific gain in accuracy
depends on the quality of the variance/covariance data available for the
specific currencies required. One can expect with reasonable confidence that the
gain will be a significant one.
While our final proposal is somewhat ahead of the current regulatory environment in terms of being an accounting tool, it can nevertheless be positioned as a front-office analytical tool to address a clear and necessary business need. Ultimately, any P/L hits as a result of deferring an incorrect amount will need to be absorbed by the front office. It is in the front office’s interest to be able to compare the results of any deferral calculations performed by the back office against statistical accounting analysis. Some legitimate questions from the management are:
We have also shown that hedge accounting, when misused, can create more problems than it solves. The key lesson to be learnt from conducting these analyses is that, if you hedge correctly and defer the correct amount, hedge accounting automatically follows. It helps you smooth earnings by building up a just enough deferral reserve. Applying the correct approach will lead to favorable tax treatment as well as consistency in overall risk and hedging analysis.
Bernard Lee is a Financial Engineer at Infinity, A SunGard Company and a Ph.D. student in Quantitative Finance at the Management School of Imperial College, London.
The author would like to thank Dr. Alvin Kuruc and Josie Palazzolo for their comments and encouragement.
Notes
1. Please refer to Alvin Kuruc, Bernard Lee,
and Alastair Wilkins, "On Hedge Effectiveness and Risk Decomposition",
Proceedings of IEEE/IAFE Conference on Computational Intelligence for Financial
Engineering, (March 28-30, 1999, New York City) pp. 297-321 for an introduction
to the mathematics of Infinity HedgeCORRect(tm).
2. Paragraph
68, SFAS 133, p.46
3. Paragraph 62, SFAS 133, p.44.
4. Robert Litterman, "Hot Spots(tm) and Hedges," Risk Management
Series, Goldman, Sachs & Co., October 1996.
5. Based on
the formula above, 1-(1-(0.8)^2)^0.5 = 0.4.
6. Paragraph 379,
SFAS 133, p.174.
7. Paragraph 380, SFAS 133, p.174.
8. Paragraph 367, SFAS 133, p.170.
9. Interested
readers may refer to the Mexicana de Cobre case study at http://www.trinity.edu/rjensen/acct5341/speakers/133sp.htm.
10. An illustration based on real-life market data will be
included in the forthcoming Infinity Financial Engineering Guide to FAS
133/IAS39 Compliance: A System Implementation Perspective.
11. Relative to the typical damping factors chosen by
RiskMetrics(r).
Monte Carlo Methods in Financial Engineering |
 |
Mathematics for Finance: Intro to Financial Engineering |